By Daniel Marantika, BIDUK Indonesia Business Development Manager

In calculating interest, both loan interest and savings interest, there are two approaches, namely:

• Nominal annual interest rate

• Effective annual interest rate

Nominal interest is interest that is calculated before inflation and is commonly the interest shown in the brochure, without taking into account other costs or compounding effects. Effective annual interest is the interest that is calculated by taking into account the compounding effect; or you could say it is the actual interest value paid (if in the form of a loan) or received (if in the form of savings).

Compounding is an effect in which the interest calculated for the current period is calculated as part of the principal value (principal), where the current period interest will be calculated as part of the principal amount for the calculation of interest in the next period.

In the table below, you can see an example scenario for a loan worth IDR 100,000,000 with a nominal interest rate of 12.00% per year, and it is calculated as compounding on a monthly basis.

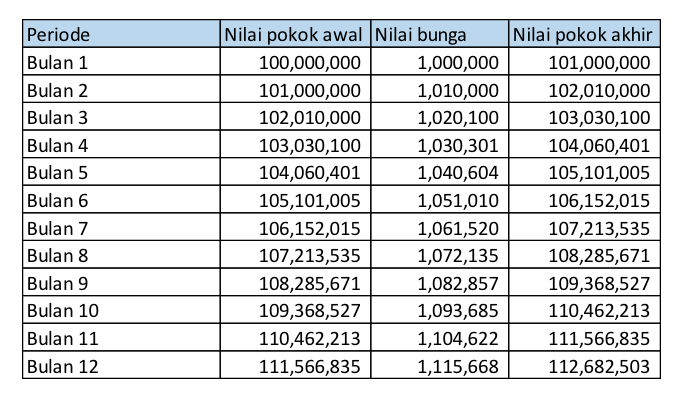
Effective interest can be calculated with the following formula:

(Final principal value – initial principal amount) / nominal interest value

Based on the table, we can see that the effective interest rate is as follows:

(IDR 112,682,503 – IDR 100,000,000) / IDR 100,000,000 = 12.68%

It can be seen that the effective interest in this scenario is greater than the nominal rate, because the interest is compounded on a monthly basis. The calculation of effective interest is important for understanding the actual value of the loan interest paid or the interest on deposits received.

Formula for calculating effective interest

To calculate the effective interest rate, the following information is required:

• The nominal interest rate stated

• Number of compounding periods (if interest is paid monthly, the value of the compounding period is 12)

Effective Interest Rate = (1 + nominal interest rate / compounding period) ^ compounding period – 1

So, with a stated nominal rate of 15%, for example, it will look like this: (1 + 15% / 12) ^ 12 – 1 = 16.08%

Just like the calculation example shown in the previous table, the effective interest value is higher than the stated nominal interest value.

How BIDUK Indonesia helps your business make better financial decisions

BIDUK Indonesia is committed to providing transparent funding and putting our clients’ priorities first, in accordance with the Smart Campaign rules (www.smartcampaign.org). We believe that honest and transparent funding will help our clients manage their finances better.